Професорот Дејан Трајковски од Битола, направи симулација со објаснување, што би се добило со евентуален 96 часовен карантин, без излегување од дома, како мерка против растечкиот број на нови позитивни во овој таканаречен трет бран од ковид пандемијата:

„Есента видовме една упростена симулација за тоа како функционира тоталниот локдаун за време на четиридневен продолжен викенд.

Да ги видиме сега пресметките со земање во предвид на точната дистрибутивна функција на веројатноста на серискиот интервал (времето од покажување на симптоми на примарниот заразувач до покажување симптоми на заразениот), прикажана на втората слика.
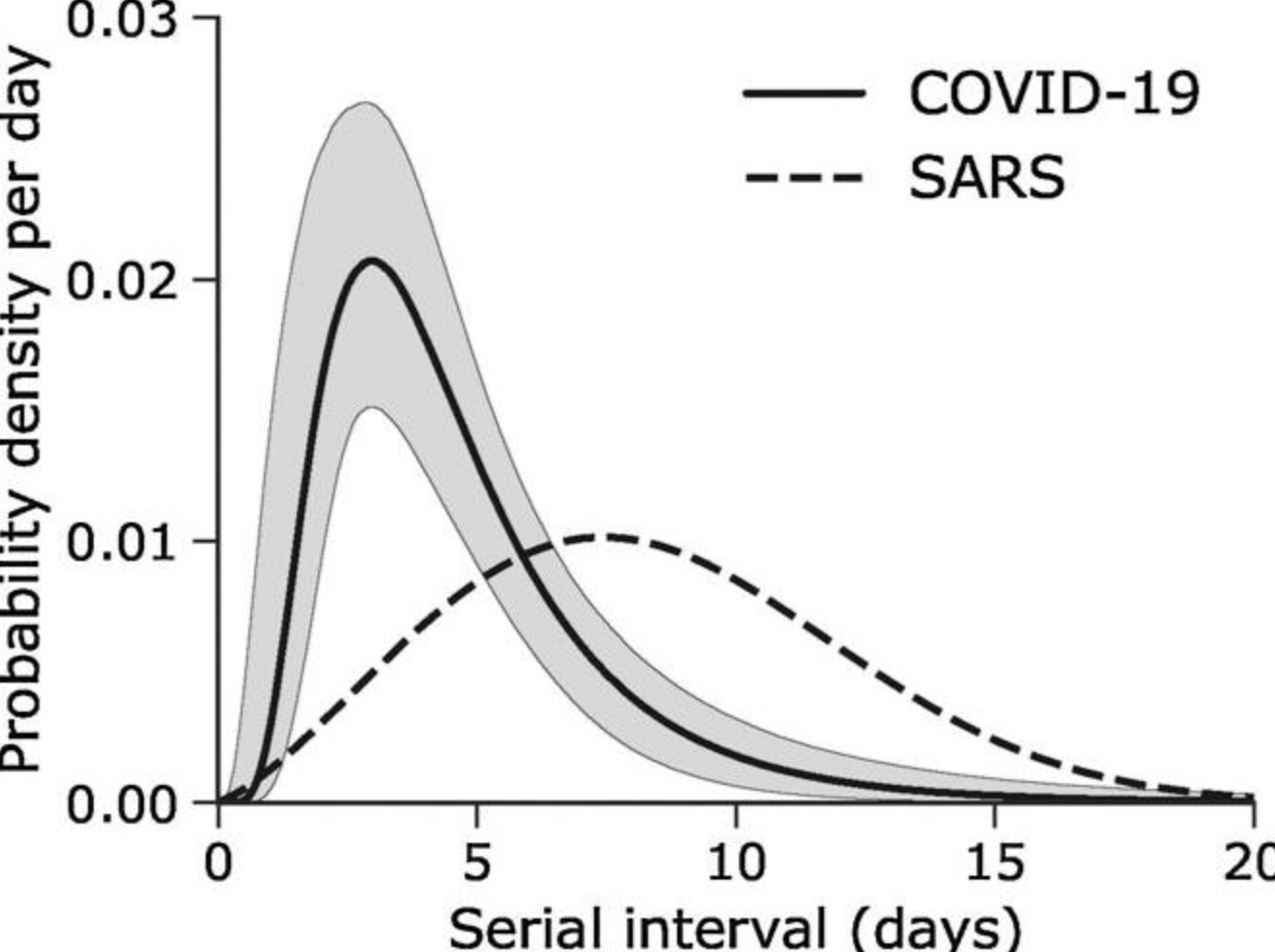
Ќе сметаме дека за време на викенд локдаунот тие што ќе покажат симптоми нема да ја пренесат заразата на други (освен евентуално на домашните), поради целосно прекинатите контакти со околината. Значи, се работи за тотален 96 часовен локдаун без излегување од дома.
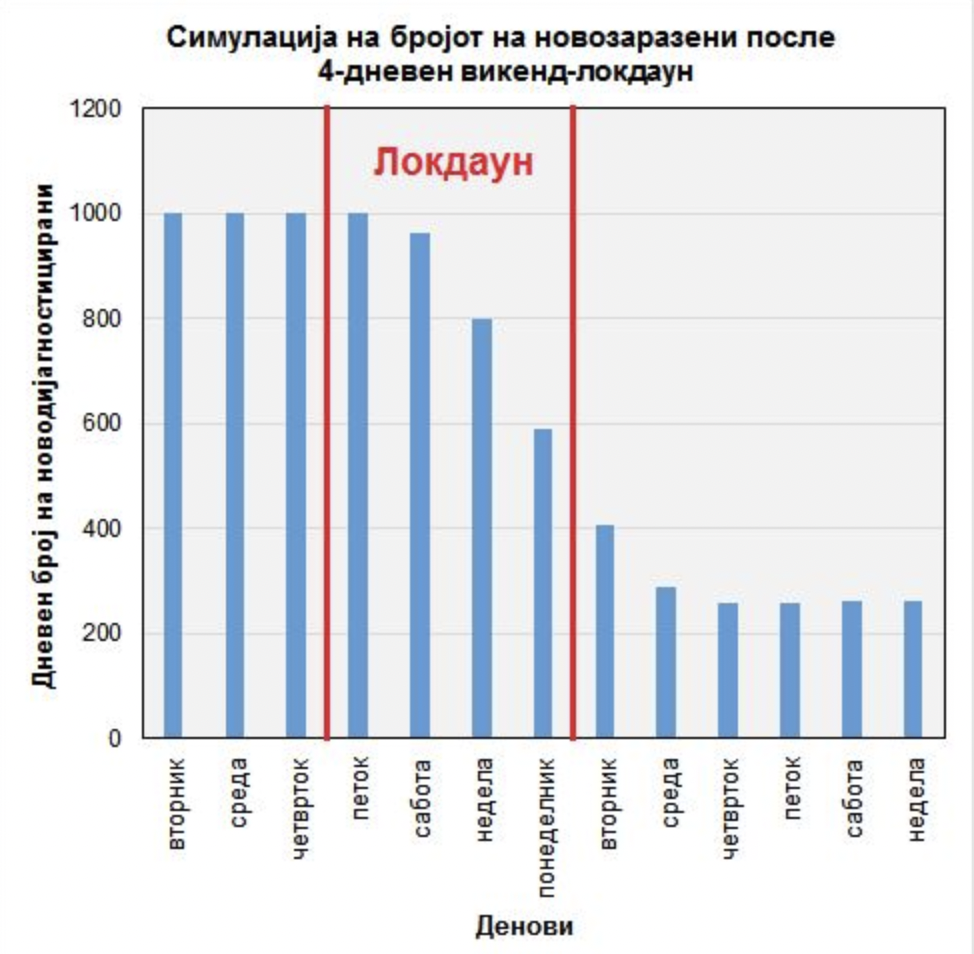
Понатаму ќе претпоставиме дека средниот дневен број на нови случаи пред локдаунот изнесувал 1.000, колку што имаме деновиве. На третата слика е прикажан дел од табелата со пресметките, додека на првата слика се прикажани резултатите.
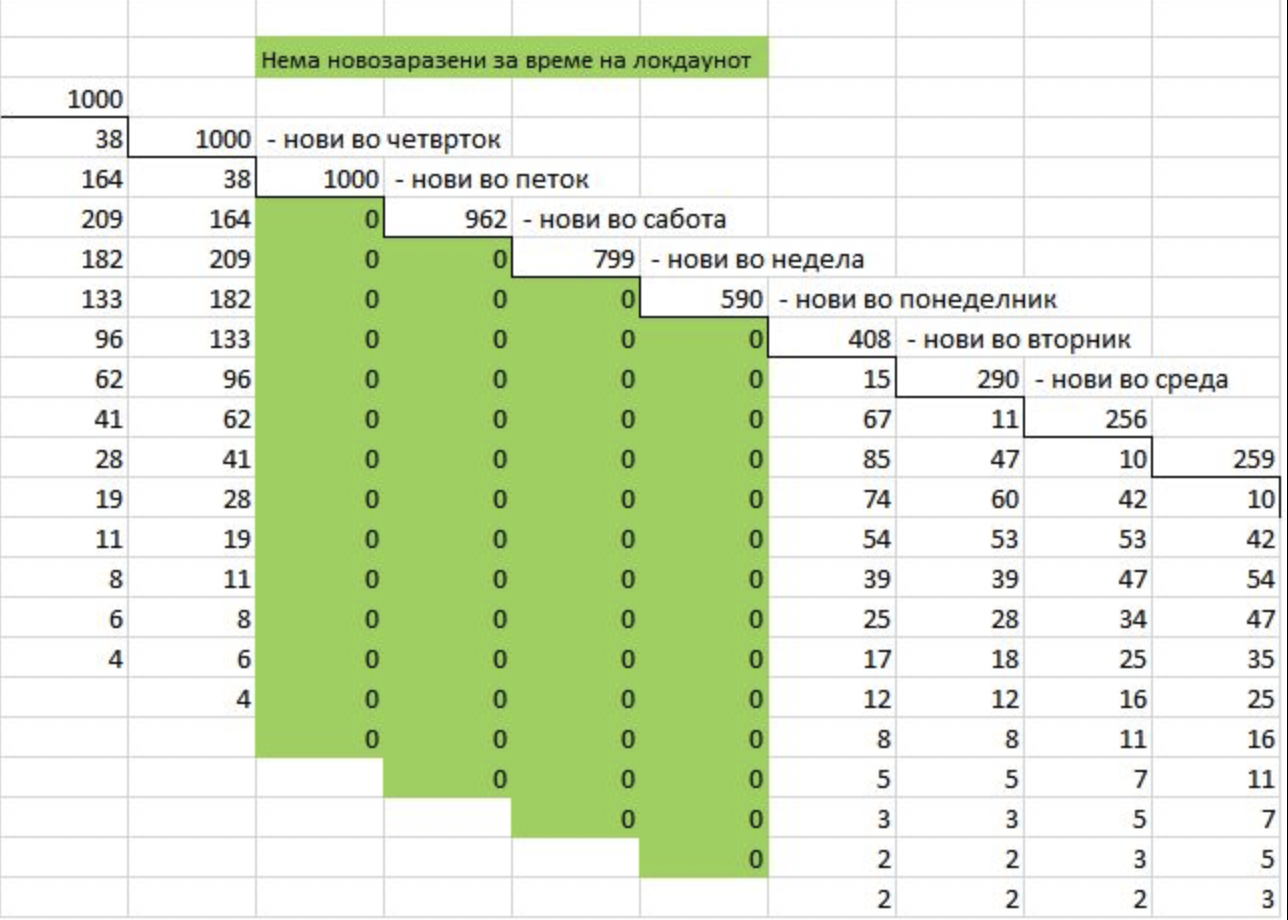
Како што се гледа од дијаграмот на првата слика, во саботата и неделата одвај да има намалување на броевите на нови случаи – тогаш практично излегуваат на виделина тие коишто се заразиле пред петокот.

Всушност, заради доцнењето на резултатите од тестирањата, нема да има видливо намалување на бројките пред вторникот. Најголемото намалување е од понеделникот до средата после локдаунот, кога бројките на нови случаи би опаднале од просечно 1.000 пред викендот на помалку од 300 после локдаунот.
Ова е под претпоставка дека ефективниот репродукционен број изнесува Rt=1. Доколку Rt е над единица бројките од среда би започнале одново полека да растат, но во апсолутни бројки растот ќе биде повеќе од три пати помал отолку пред локдаунот.

Нормално, не е исто дали заразата ја пренесуваат 1.000 или само 260 лица дури при истата преносливост.

Од понеделникот понатаму би се продолжило со сегашните рестриктивни мерки, со евентуално дополнително скратување на работното време на кафеаните.

Откако населението ќе се одмори од локдаунот, по две недели да се повтори локдаунот и бројките да се соборат на помалку од 100.

Доколку бројките потоа одново забегаат нагоре (да речеме над 300 дневно), според овој алгоритам да се притиска на сопирачката и да не се дозволува нов неконтролиран раст.
Во меѓувреме населението масовно да се вакцинира и така да се стави крај на епидемијата. Толку е едноставно, ова не е атомска физика!

Забелешка: дистрибутивната функција на втората слика важи за старите соеви на вирусот, за британскиот сој серискиот интервал е во просек уште пократок. Како резултат на ова скратување и соборувањето на бројките би било побрзо и поголемо.